Les Hexamys et l'Orthogonalité

                   La lecture de ces lignes suppose la lecture préalable des pages précédentes dans lesquelles nous avons fait connaissance avec la géométrie inventée par Poncelet, puis avec le beau théorème de Pascal, et enfin avec la résolution par les hexamys des problèmes de géométrie faisant intervenir des droites parallèles. Il nous reste à présent à voir comment cette méthode permet aussi de traiter les problèmes qui font intervenir des droites perpendiculaires.

 

                    Parmi les figures de la géométrie euclidienne qui contiennent des angles droits, intéressons nous au carré car il contient deux orthogonalités : celle de ses cotés et celle de ses diagonales. Dans l'histoire de Poncelet qui projetait sur la buée de sa vitre les traces qu'il voyait sur la neige, imaginons qu'une grande bache carrée ABCD se soit trouvée sur la neige, et que Poncelet l'ait pareillement projetée sur la vitre. Voilà à peu prés le dessin qu'il aurait eu:

                    En utisant le langage de la géométrie projective qui nous est à présent familier nous disons que les droites paralléles AD et BC se coupent sur la droite de l'infini en P' et que les droites parallèles AB et DC se coupent sur la droite de l'infini en P.

                    Or dans le carré ABCD les cotés AB et CD sont perpendiculaires aux cotés AD et BC. Alors notre langage projectif va encore s'enrichir d'une nouvelle définition : nous dirons que toutes les droites passant par P ( donc paralléles entre elles au sens projectif) sont perpendiculaires au sens projectif à toutes les droites passant par P' ( donc elles aussi paralléles entre elles au sens projectif) . Et pareillement nous dirons que toutes les droites passant par Q sont perpendiculaires au sens projectif à toutes les droites passant par Q'.

                    Et alors, ce qui est tout à fait surprenant, c'est que la donnée de ces quatre points alignés P,P',Q et Q' suffit à déterminer non seulement les deux perpendicularités qu'on vient de voir, mais aussi, au sens projectif, toutes les autres perpendicularités du plan. En effet, sur la figure ci dessous, supposons donnés un point A et une droite d quelconques du plan, et proposons nous de construire ce que serait au sens projectif la droite perpendiculaire à la droite d menée par A.

                    Par A nous menons les droites AP et AQ qui coupent la droite d respectivement en B et C . Puis on mène les droites CP' et BQ'. D'après ce que nous avons vu plus haut les droites BP et CP' sont donc perpendiculaires au sens projectif du terme, de même que les droites CQ et BQ'. Par conséquent elles sont les hauteurs, toujours au sens projectif du terme, du triangle ABC et par suite elles se coupent en son orthocentre H. Par conséquent, encore au sens projectif du terme, la droite AH est la troisième hauteur du triangle ABC et par conséquent nous allons convenir de dire qu'elle est perpendiculaire, au sens projectif du terme à la droite d.

                    Ainsi une droite d étant donnée et coupant la droite de l'infini en M nous savons lui associer le point M' de cette droite de l'infini tel que les directions passant par M soient perpendiculaires au sens projectif aux directions passant par M'. En effet il suffit avec deux points B et C de cette droite de construire les intersections A de CQ et BP , puis H de CP' et BQ'.

                    Dans la vulgarisation présentée ici , il n'est évidemment pas question de traiter toutes les questions que pose l'orthogonalité ainsi introduite. Qu'on sache cependant que par les hexamys on les résoud toujours aussi facilement.

                  Donnons un exemple: Cherchons par exemple si,(voir figure ci dessous) lorsqu'une droite issue d'un point A est perpendiculaire à une droite d, cette droite est bien aussi perpendiculaire à toute droite d' paralléle à d.

                    Puisque les droites d et d' sont paralléles, c'est qu'elles se coupent en un même point à l'infini. Soit M ce point. Le problème est alors de savoir, dans les deux triangles ABC et AB'C', si AH est bien la même droite que AH', c'est à dire si les trois points A,H, et H' sont alignés. Ici c'est un joli hexamys qui donne la solution:

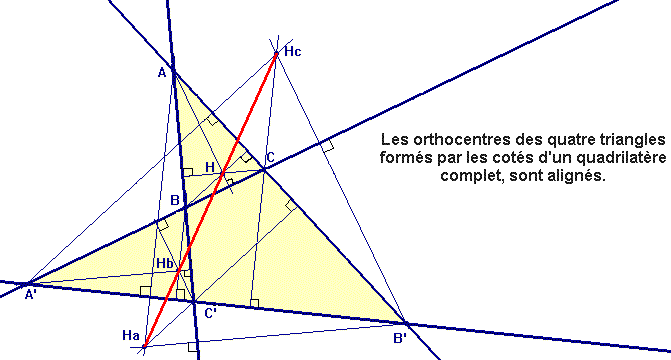
et on vérifie ainsi cette propriété caractéristique bien connue: si deux droites sont parallèles toute perpendiculaire à l'une est aussi perpendiculaire à l'autre.

                    Dans la page "parallélisme" nous avons vu que nous savons déterminer le milieu d'un segment AB. Ici nous voyons que par ce milieu nous savons mener la droite perpendiculaire à AB qui est donc sa "médiatrice" au sens projectif. Tout point de cette médiatrice forme avec A et B un triangle isocèle au sens projectif. Et ainsi de suite, les problèmes de cohérence et de compatibilité continuant à se résoudre par les hexamys.

                  On pourra donc encore résoudre par les hexamys de nombreux problèmes faisant aussi intervenir l'orthogonalité.

                    Pour en donner un exemple, démontrons que les quatre triangles déterminés par les côtés d'un quadrilatère complet ont leurs orthocentres alignés. Comme on le voit il s'agit d'un problème assez compliqué, et nous sommes bien en géométrie euclidienne puisqu'il y est question d'orthocentres.Voici la figure:

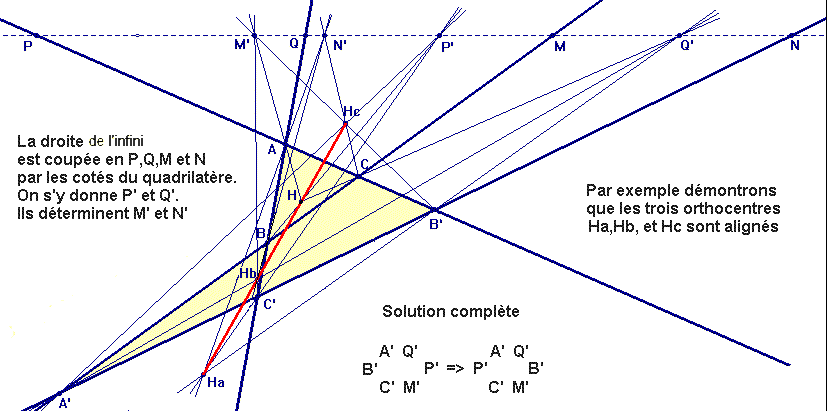
                    Pour faire cette démonstration nous allons comme d'habitude nous transposer en géométrie projective. Nous savons maintenant que dans cette géométrie, grâce aux hexamys, les démonstrations sont faites en douze lettres. Voilà alors ci dessous la figure de ce même problème dessinée en géométrie projective:

                    On se choisit une droite de l'infini arbitraire. Soient P,Q,M et N les points où elle est coupée par les cotés du quadrilatère complet ABCA'B'C'. On se donne arbitrairement les points P' et Q' sur cette droite de l'infini pour déterminer comme on l'a vu plus haut une orthogonalité au sens projectif . Dés lors on peut tracer les trois hauteurs du triangle ABC et les trois hauteurs du triangle AB'C' qui nous définissent deux autres orthogonalités par les couples de points M et M' puis N et N' sur la droite de l'infini.

                    C'est alors un hexamys élémentaire ( A'B'C' alignés et P'Q'M' alignés) qui montre par exemple que les trois orthocentres Ha du triangle AB'C', Hb du triangle BC'A' et Hc du triangle CA'B' sont alignés, laissant pour le moment l'orthocentre H de ABC de coté. Mais on raisonnerait de la même façon en laissant de coté Ha ou Hb ou Hc ce qui montre bien que ces quatre orthocentres sont alignés.

                    Il est évidemment inutile de multiplier les exemples. Le processus des démonstrations dans l'esprit de ce site est dorénavant suffisamment clair. Un problème étant donné en géométrie euclidienne on le décompose en étapes élémentaires puis on traite chacune de ces étapes par les hexamys après les avoir exprimées en géométrie projective.

Conclusion

                    Sur les traces de Poncelet, en imaginant que nous étions le Bon Dieu et que la droite de l'infini est une droite comme les autres, nous avons découvert une géométrie bien plus simple que la géométrie euclidienne puisqu'elle ne nécessite que l'usage de la règle, alors que la géométrie euclidienne nécessite l'usage de la règle et du compas.

                    Ensuite grâce aux belles propriétés de l'Hexagramme Mystique de Pascal nous avons découvert une merveilleuse méthode de résolution et de rédaction des problèmes de géométrie puisqu'elle ne nécessite en tout et pour tout que l'écriture de douze lettres ce qui est absolument extraordinaire.

                    Et enfin nous avons vu que les énoncés obtenus en géométrie projective peuvent traduire des énoncés de géométrie euclidienne si on accepte de poser deux conventions. La première c'est d'appeler parallèles les droites qui se coupent sur une droite du plan arbitrairement choisie comme droite de l'infini. La deuxième c'est d'appeler perpendiculaires les droites obtenues par la construction précédente à partir de quatre points arbitrairement donnés sur la droite de l'infini.

                    Il est évident que dans cette présentation exposée de façon volontairement sommaire pour être accessible à de jeunes adolescents, de nombreux détails nécessaires dans une étude véritablement approfondie ont été passés sous silence. En particulier le choix des couples P et P' puis Q et Q' pour déterminer une orthogonalité compatible avec celle de la géométrie euclidienne n'est pas absolument arbitraire. Il faut que les segments [PP'] et [QQ'] se recouvrent partiellement, comme dans les suites PQP'Q' ou PQ'P'Q par exemple.

                    Mais ces quelques lignes suffiront à ceux qui le désirent pour avoir une idée de cette belle Géométrie Projective ignorée de nos programmes à tel point que des Thèorèmes aussi merveilleux que ceux de Desargues, de Pappus et même de l'Hexagramme Mystique de Pascal sont tout simplement ignorés, non seulement de la plupart de nos étudiants, mais bien souvent aussi de nombreux professeurs. Pour ceux chez qui cette vulgarisation sommaire aura pourtant réussi à susciter l'intérèt, ils pourront trouver une étude approfondie chez le grand spécialiste de la Géométrie Projective que fut le professeur italien Federigo ENRIQUES.

                    Il fut en particulier en 1930 l'auteur du livre: Leçons de Géométrie Projective dans lequel on lit ( p 46 ) qu'en se servant du Théorème de Desargues qu'il appelle Théorème des Triangles Homologiques [ NDLR: il aurait été plus exact de le remplacer par Pappus] " on pourrait déduire tous les théorèmes de géométrie projective " ce qui confirme bien que par les Hexamys on peut déduire tous les théorèmes de Géométrie Projective puisque le Théorème des Hexamys contient justement celui de Desargues et aussi celui de Pappus.

                    Et à la page 274 de ce même livre il confirme que par la géométrie projective on peut retrouver beaucoup des propriétés métriques de la géométrie euclidienne puisque il écrit " ...en particulier on pourra résoudre, en se servant seulement de la règle, tous les problèmes métriques du premier degré. Parmi ces problèmes, ceux qui sont relatifs à la construction de la paralléle ou de la perpendiculaire menée par un point à une droite donnée, sont particulièrement typiques..." .

                    Le mot important est évidemment ici " les problèmes métriques du premier degré ". Par exemple l'axiome III1 de D Hilbert pour la géométrie euclidienne impose: Si A et B sont deux points d'une droite a, et si A' est un point de cette droite ou d'une autre droite a', alors, sur a', d'un coté de A' on peut trouver un point B' tel que le segment AB soit congruent au segment A'B' [source Les fondements de la Géométrie par D Hilbert / Dunod 1971]. Or si les droites a et a' sont confondues ou parallèles nous avons vu dans la page parallélisme qu'on sait effectivement définir une telle congruence, mais elle nous est impossible en géométrie projective si les droites a et à sont sécantes. C'est le seul bémol pour les merveilleuses possibilités de l'hexagramme mystique. Mais il faut reconnaître qu'effectivement, il est de taille.

  Retour à l'accueil